参考链接：

[1] 邱锡鹏：神经网络与深度学习

[2] Jay Alammar：Illustrated Transformer

[3] 深度学习-图解Transformer(变形金刚)

[4] 详解Transformer

自注意力

在讲述Transformer之前，首先介绍Self-Attention模型。

传统的RNN虽然理论上可以建立输入信息的长距离依赖关系，但是由于信息传递的容量和梯度消失的问题，实际上只能建立短距离（局部）依赖关系。为了建立输入序列之间的长距离依赖关系，并利用注意力机制来“动态”地生成不同连接的权重，诞生了自注意力模型(Self-Attention Model)

自注意力模型采用查询-键-值(Query-Key-Value,QKV)模式，计算过程如下图，红色字母表示维度：

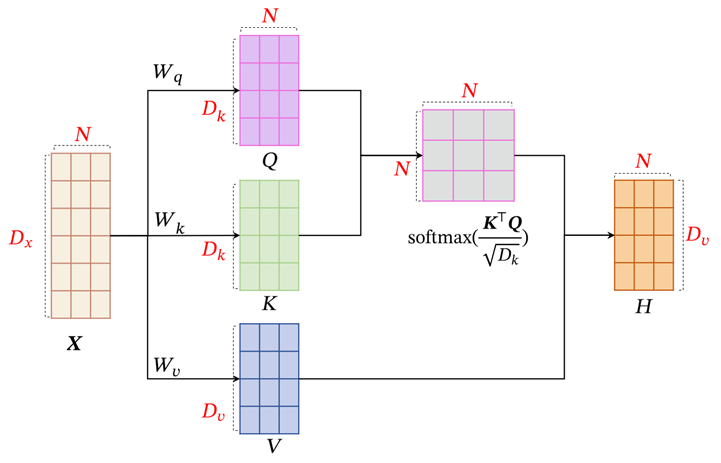
计算过程：

• 输入序列

• 生成三个向量序列：

  $$\begin{align} \boldsymbol{Q}=\boldsymbol{W}_q \boldsymbol{X} \in \mathbb{R}^{D_k \times N} \tag{1}\\ \boldsymbol{K}=\boldsymbol{W}_k \boldsymbol{X} \in \mathbb{R}^{D_k \times N} \tag{2}\\ \boldsymbol{V}=\boldsymbol{W}_v \boldsymbol{X} \in \mathbb{R}^{D_v \times N} \tag{3} \end{align}$$

  其中，，，分别为线性映射的参数矩阵，，，分别是由查询向量、键向量和值向量构成的矩阵。

  注意：Self-Attention中通常使用点积来计算注意力打分，这里的查询向量Q和键向量K的维度是相同的。

• 最终的输出序列是，其中的输出向量使用键值对计算方法计算：

  $$\begin{align} \boldsymbol{h}_n &= \mbox{att}((\boldsymbol{K},\boldsymbol{V}),\boldsymbol{q}_n)\\ &=\sum_{j=1}^N \alpha_{nj} \boldsymbol{v}_j \\ &=\sum_{j=1}^N \mbox{softmax}(s(\boldsymbol{k}_j,\boldsymbol{q}_n)) \boldsymbol{v}_j \tag{4} \end{align}$$

  其中为输出和输入向量序列的位置，表示第个输出关注到第个输入的权重。

• 如果使用缩放点积来作为打分函数的话，输出向量序列可以简写为：

  $$\boldsymbol{H}=\mbox{softmax}(\frac{\boldsymbol{Q} \boldsymbol{K}^T}{\sqrt{D_k}}) \boldsymbol{V} \tag{5}$$

公式(5)的写法中，softmax函数按行进行归一化，即每一行进行归一化，归一化方法根据公式的写法决定。

自注意力模型可以作为神经网络的一层来使用，既可以用来替换卷积层和循环层，也可以和它们一起交替使用。

由于自注意力模型的权重只依赖于和的相关性，忽略了输入信息的位置信息，因此单独使用时，一般需要加入位置编码信息进行修正，Transformer中就是这么做的。

多头自注意力

多头自注意力(Multi-Head Self-Attention)在多个不同的投影空间中捕捉不同的交互信息。假设在M个投影空间中分别应用自注意力模型，则：

其中，，，，为投影矩阵，.

也就是说，多头自注意力是将多个不同参数的自注意力的结果进行拼接，如图：

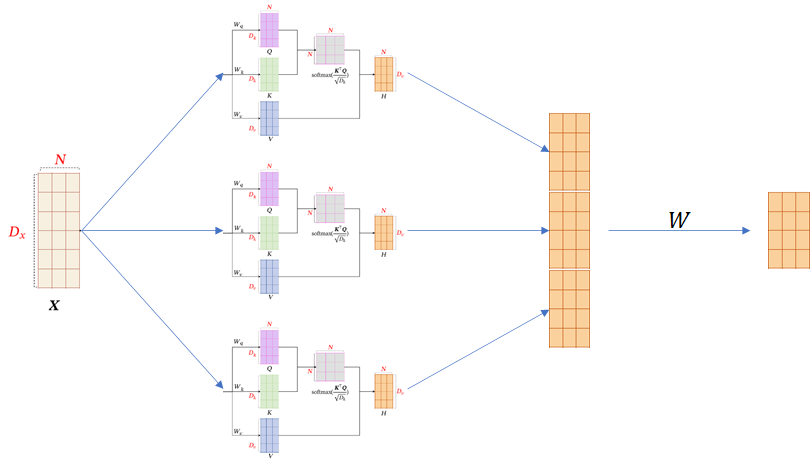
Transformer

Transformer是2017年Google团队提出的一个基于Mult-Head Attention的Seq2Seq模型，整个网络结构由编码器和解码器两部分组成，原文链接Attention Is All you Need.

Transformer的主要结构如下：

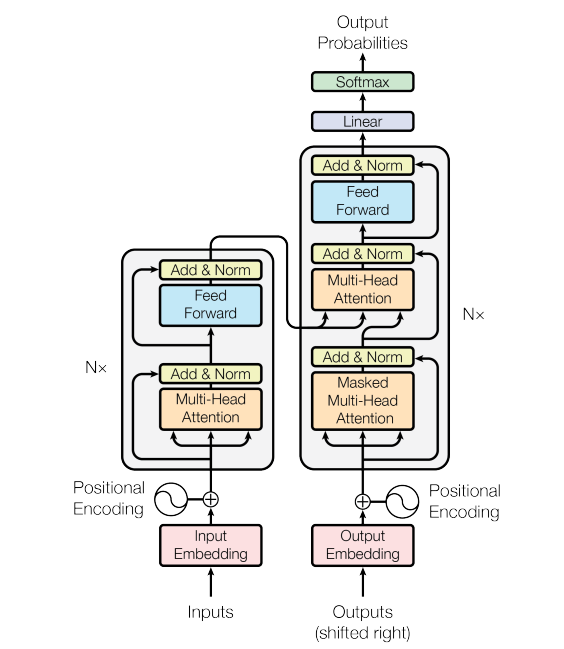
上图是来自原文的结构图，左边是N个编码器，右边是N个解码器，Transformer中的N为6，下图是Jay Alammar博客中的简化图：

编码器

Transformer中的编码器部分一共有6个相同的编码器层组成，下面以单个层为例。如下图，每个编码器都有两个子层，即多头自注意力层(Multi-Head Attention)层和逐位置的前馈神经网络(Position-wise Feed-Forward Network)。在每个子层后面都有残差连接（图中的虚线）和层归一化（LayerNorm）操作，二者合起来称为Add&Norm操作。

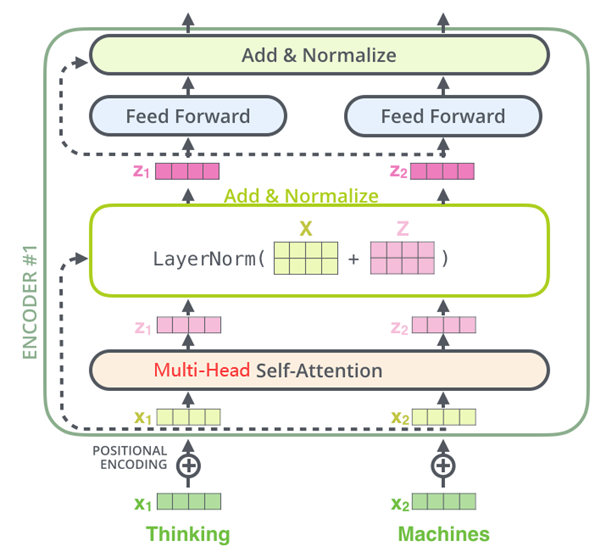
编码器的输入为序列，输出为，然后用两个矩阵将映射到和作为键值对供解码器使用：

编码器中的关键步骤：

1. 位置编码

   由于自注意力模型忽略了序列中每个的位置信息（即使句子结构混乱也能得到类似的结果），因此需要在初始的输入序列中加入位置编码来进行修正，对于输入序列，令：

   $$\boldsymbol{H}^{(0)} = [\boldsymbol{e}_{x_1}+\boldsymbol{p}_1,\ldots,\boldsymbol{e}_{x_T}+\boldsymbol{p}_T] \tag{11}$$

   其中是词的嵌入向量表示，是位置 的向量表示，即位置编码。位置编码通过下面的公式预定义：

   $$\begin{align} \boldsymbol{p}_{t,2i} &=\sin (\frac{t}{10000^{\frac{2i}{D}}}) \\ \boldsymbol{p}_{t,2i+1} &=\cos (\frac{t}{10000^{\frac{2i}{D}}}) \tag{12} \end{align}$$

   其中表示第个位置的编码向量的第维，是编码向量的维度。

   Transformer里的位置编码是没有梯度的，不参与训练，每个位置上的值是固定的。

1. 层归一化和残差连接(Add&Norm)

   每个子层后都跟着Add&Norm层，包括残差连接和层归一化操作：

   $$\mbox{LayerNorm}(\boldsymbol{X}+\mbox{Sublayer}(\boldsymbol{X})) \tag{13}$$

   其中是来自上个子层的输出，表示层归一化操作，表示上个子层的函数，即或者.

   Transoformer中的子层和Add&Norm层之间有dropout操作。

2. 逐位置的前馈神经网络(Position-wise-Feed-Forward Network)

   逐位置的前馈神经网络是一个简单的两层网络，对于序列的每个位置上的向量执行以下操作：

   $$\mbox{FFN}(\boldsymbol{x})=\boldsymbol{W}_2 \mbox{ReLu}(\boldsymbol{W}_1\boldsymbol{x}+\boldsymbol{b}_1)+\boldsymbol{b}_2 \tag{14}$$

解码器

解码器部分同样由6个相同的层组成，每层都采用自回归的方式生成目标序列，接收来自编码器的输出和，以及上一层解码器的输出（用来生成查询向量）。同样以单层为例，每层包括三个子层：掩蔽自注意力层(Masked Self-Attention)、Encoder-Decoder注意力层、逐位置的前馈神经网络，同样，每个子层后面都有Add&Norm操作，具体结构如图：

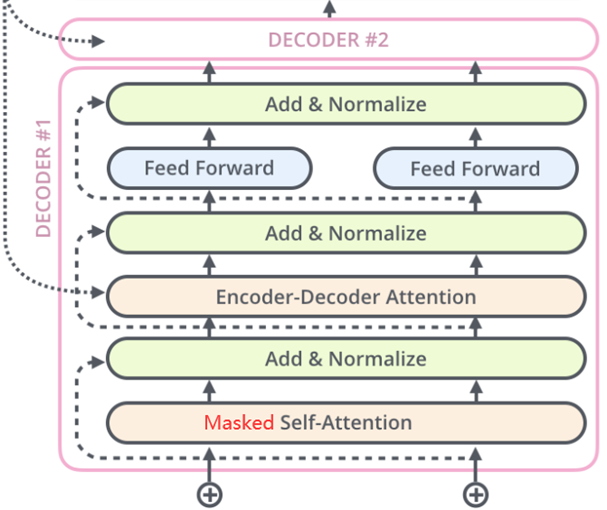
解码器中的关键步骤：

1. 掩蔽自注意力 (Masked Self-Attention)

   第步时，使用掩蔽自注意力模块对已经生成的前缀序列进行编码，得到，使之后的序列不可见。

2. Encoder-Decoder注意力

   将进行线性映射得到，将作为查询向量，通过键值对注意力机制，来从输入(，)中选取有用的信息。

3. 逐位置的前馈神经网络

   同编码器的网络，用来综合得到所有的信息。

与编码器一致，解码器也包括层归一化、残差连接的操作，其计算方式也相同，这里不再具体介绍。

解码器的解码过程可以参考下图：

然后重复以上步骤，直到句子结束：

解码器初始的输入要有起始符来激活解码器，这里用<s>表示(上图中没体现)，起始符是通过右移(shifted right)操作事先给定好的。结束符用p表示。将图中的例子用语言描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

Step 1
起始输入：起始符<s>+p
中间输入：K、V
最终输出：I

Step 2
起始输入：起始符<s>+'I'+p
中间输入：K、V
最终输出：I am

Step 3
起始输入：起始符<s>+'I'+'am'+p
中间输入：K、V
最终输出：I am a

Step 4
起始输入：起始符<s>+'I'+'am'+'a'+p
中间输入：K、V
最终输出：I am a student

Step 5
起始输入：起始符<s>+'I'+'am'+'a'+'student'+p
中间输入：K、V
最终输出：I am a student <end of sentence>

补充说明：

1. 关于掩蔽自注意力：

   在训练过程中，为了能够一次性完成以上步骤以提高效率，将右移的目标序列(Right-Shifted Output) 作为解码器输入， 即在第个位置的输入为，通过掩码(Mask)来阻止每个位置选择后面的输入信息，只能看到之前的解码结果，这种方法就称为掩蔽自注意力(Masked Self-Attention)。例如，一个3*3的矩阵，矩阵的每一行对应于解码的每一步：

   $$\mbox{Mask}: \left[ \begin{array} {cccc} 1&0&0&0\\ 1&1&0&0\\ 1&1&1&0\\ 1&1&1&1\\ \end{array} \right]$$

   而在测试/预测过程中，解码过程是一步一步计算的。每一步中解码器输出的矩阵取最后一行用来预测下一个词。

2. 关于右移(Shifted Right)操作

   右移操作是为了在编码器的初始输入中添加起始符<s>,例如，正常的输出序列位置关系：

   1 2 3 4

   0:'I' 1:'am' 2:'a' 3:'student'

   通过右移操作后的输入序列：

   1 2 3 4 5

   0:<s> 1:'I' 2:'am' 3:'a' 4:'student'

总结

参考链接[4]的内容，说明了Transformer的优缺点：

优点：

• Transformer设计足够有创新，其抛弃了在NLP中最根本的RNN或者CNN并且取得了非常不错的效果。
• Transformer的设计最大的带来性能提升的关键是将任意两个单词的距离是1，这对解决NLP中棘手的长期依赖问题非常有效。
• Transformer不仅可以应用在NLP的机器翻译领域，还可以应用在其他非NLP领域。
• Transformer算法并行性很好，符合目前硬件(主要指GPU)环境。

缺点：

• 粗暴的抛弃RNN和CNN使模型丧失了捕捉局部特征的能力，RNN + CNN + Transformer的结合可能会带来更好的效果。
• Transformer失去的位置信息在NLP中非常重要，而论文中在特征向量中加入Position Embedding只是一个权宜之计，并没有改变Transformer结构上的固有缺陷。