友情参考：邱锡鹏老师的神经网络与深度学习

注意力机制

在计算能力有限的情况下，注意力机制(Attention Machanism)作为一种资源分配方案，将有限的计算资源用来处理更重要的信息，是解决信息过载问题的主要手段。通俗来说，注意力机制就是只关注和当前需求相关的信息，以阅读理解为例，对于给定的问题，只需要关注和问题相关的一个或几个句子，其余无关的部分不需要关注。

数学思想表达：表示N个输入信息，为了节省计算资源，只需要中选择一些和任务相关的信息进行计算。

注意力的计算

一般情况下，我们使用的是Soft Attention，即各种信息的加权平均。还有一种Hard Attention，下文会讲。

为了从N个输入向量中选择出与任务相关的信息，需要引入和任务相关的表示，称为查询向量(Query Vector)，并通过一个打分函数计算每个输入向量和查询向量之间的相关性。

查询向量q可以是动态生成的，也可以是可学习的参数。

Soft Attention机制示例如下：

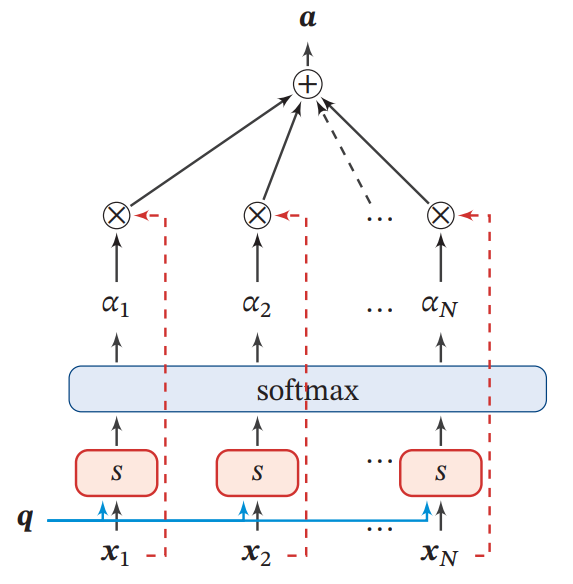
给定查询向量和输入信息，根据“软性”的信息选择机制对输入信息进行汇总：

上式中的称为注意力分布，表示在给定和情况下，选择第个输入向量的概率，也可以解释为在给定任务相关的查询时，第个输入向量受关注的程度：

其中为注意力打分函数，是注意力机制中最重要的一部分，它主要计算的是注意力分数的大小。可以通过以下几种方式计算：

• 加性（感知机）模型

  $$s(\boldsymbol{x},\boldsymbol{q})=\boldsymbol{v}^T \tanh(\boldsymbol{Wx+Uq}) \tag{3}$$

• 点积模型

  $$s(\boldsymbol{x},\boldsymbol{q})=\boldsymbol{x}^T \boldsymbol{q} \tag{4}$$

• 缩放点击模型

  $$s(\boldsymbol{x},\boldsymbol{q})=\frac{\boldsymbol{x}^T \boldsymbol{q}}{\sqrt{D}} \tag{5}$$

• 双线性模型

  $$s(\boldsymbol{x},\boldsymbol{q})=\boldsymbol{x}^T \boldsymbol{Wq} \tag{6}$$

各自的优缺点:

1. 加性模型对于大规模数据特别有效，但是训练成本较高。
2. 理论上，点积模型和加性模型复杂度差不多，但是点积模型只利用矩阵相乘，计算效率更高。
3. 输入向量维度较高时，最后得到的权重会增加，为了提升计算效率，防止数据上溢，对齐scaling，即缩放点积模型。
4. 双线性模型通过权重矩阵直接建立x和q的关系映射，比较直接且速度较快。双线性模型的公式也可以写为，与点积模型相比，计算相似度时引入了非对称性。

注意力机制的变体

硬性注意力

上面介绍的是软性注意力，其选择的信息是所有输入向量在注意力分布下的期望。此外，还有一种注意力是只关注某一个输入向量，叫作硬性注意力(Hard Attention)。

硬性注意力有两种方式：

1. 一种是选取最高概率的一个输入向量，即：

   $$att(\boldsymbol{X,q})=\boldsymbol{x}_{\hat{n}} \tag{7}$$

   其中是概率最大的输入向量的下标，即.

2. 另一种通过在注意力分布上随机采样的方式实现。

硬性注意力的缺点是基于最大采样或随机采样的方式选择信息，使得最终的损失函数与注意力分布之间的函数关系不可导，无法使用反向传播算法进行训练，因此，硬性注意力通常需要使用强化学习来进行训练，为了使用反向传播算法，一般使用软性注意力代替硬性注意力。

键值对注意力

键值对(key-value pair)注意力用表示组输入信息，给定任务相关的查询向量时，注意力函数为：

其中为打分函数，当时，键值对模式就等价于普通的注意力机制。

键值对注意力机制的示例如下图：

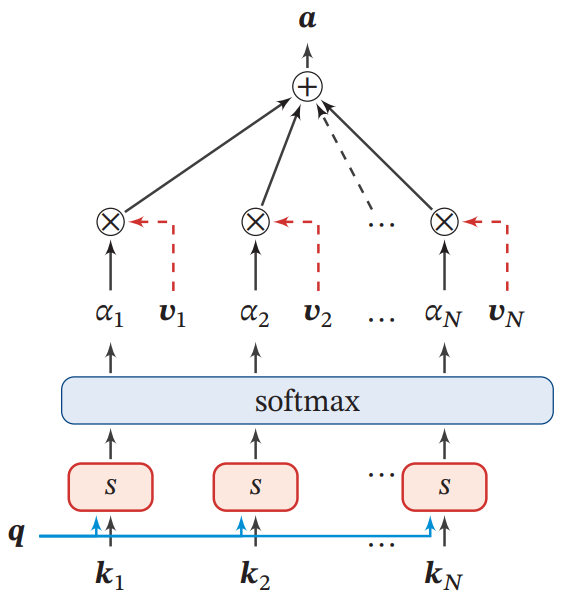
多头注意力

多头注意力(Multi-Head Attention)是利用多个查询，来并行地从输入信息中选取多个多组信息，每个注意力关注输入信息的不同表示空间：

其中表示向量拼接。

多头注意力通常用在自注意力之后，详情参见自注意力和Transformer.

指针网络

注意力机制主要是用来做信息筛选，从输入信息中选取相关的信息。注意力机制可以分为两步：一是计算注意力分布，二是根据来计算输入信息的加权平均。我们可以只利用注意力机制中的第一步，将作为一个软性的指针(poiner)来指出相关信息的位置。

指针网络是一种序列到序列模型，输入是长度为的向量序列，输出是长度为的下标序列，其中.

和一般的Seq2Seq任务不同，这里的输出序列是输入序列的下标（索引），比如输入一组乱序的数字，输出为按大小排序的输入数字序列的下标，比如输入为20,5,10，输出是1,3,2。

条件概率可以写为：

其中条件概率可以通过注意力分布来计算。

关于指针网络的详情可以参考Pointer Networks简介及其应用.