
论文阅读-Star Graph Neural Networks for Session-based Recommendation
2020年10月份CIKM会议的一篇论文,主要内容是提出了带有Highway Network的Star-GNN模型,简称为SGNN-HN模型,原文链接
摘要
现有基于GNN的模型,有两个缺陷:
- 一般的GNN模型只考虑了相邻item的转换信息,忽略了来自不相邻item的高阶转换信息。
- 一般的GNN模型,如果想要捕获高阶转换信息,必须要增加层数,这样就面临严重的过拟合问题
为了解决上述两个问题,作者提出了Star Graph Neural Networks with Highway Networks (SGNN-HN)模型:
- 对于问题1,使用Star GNN(SGNN)学习当前session中不相邻item的复杂转换信息。
- 对于问题2,使用Highway Networks(HN)自适应地从item表示中选择嵌入信息,缓解过拟合问题。
一、介绍
基于session的推荐系统是根据当前正在进行的session生成推荐,SBRS没有用户的历史交互信息,只有当前session中的item信息,并且是很有限的。使用RNN考虑session的序列信息(如GRU4Rec),或者使用注意力机制考虑主要目的(如NARM),都不能完全考虑到item的复杂转换信息。后来的GNN模型(如SRGNN、TAGNN等),虽然利用GNN的优势,考虑了item间的复杂转换信息,但是面临上述两个问题,即高阶转换信息和过拟合问题。
因此,作者提出了SGNN-HN模型,首先在图中加入star节点,构建SGNN,建立当前session复杂item转换信息的模型,解决长距离信息传播问题。然后使用HN,在SGNN前后动态选择item表示,解决过拟合问题。最后使用注意力机制将item表示融合,得到session表示,用于推荐。
二、相关工作
- 一般推荐模型:CF、MF、NCF、Item-KNN等
- 序列推荐模型:MC、FPMC、GRU4Rec、NARM、KNN、CSRM
- 注意力模型:STAMP、Co-Attention模型
- GNN模型:SRGNN、FGNN
三、本文模型
本文模型结构图如下:
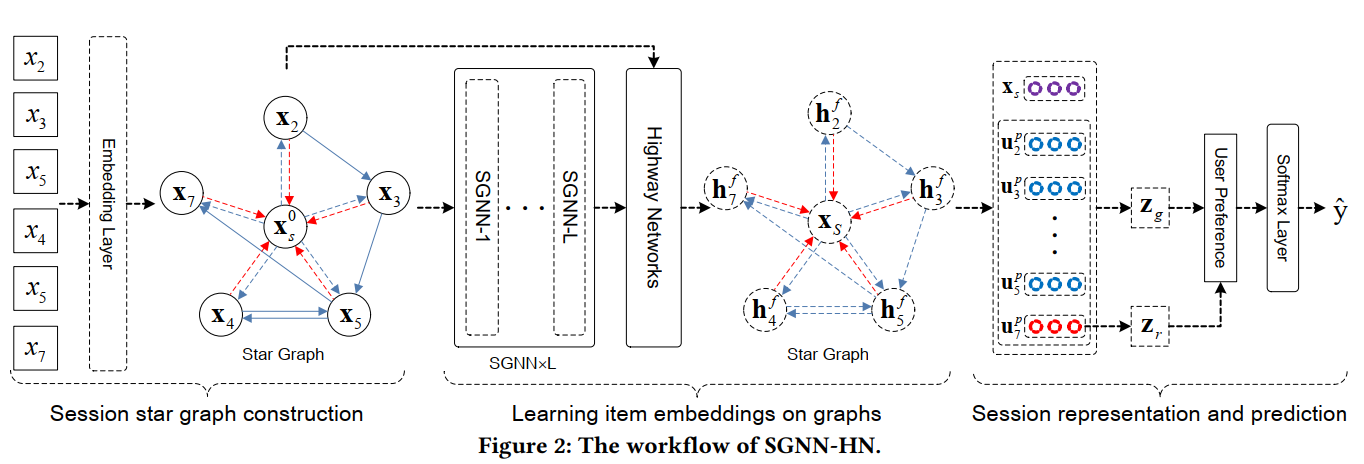
3.1 问题定义
表示所有session中的item集合,其中 表示item的个数。
是给定的当前session,包含n个item。
模型的目标是预测 ,具体来说,对于每个session,输出 ,表示所有item的预测分数,最后取分数最高的K个作为推荐item。
3.2 构建星型图
对于每个session ,构建为一个星型图,表示为。
其中表示图中的所有节点。前半部分表示satellite节点,表示star节点。注意这里的,因为session中可能会有重复出现的item。
是图中的边集合,包括satellite连接(图2中实线)和star连接(图2中虚线)两种有向边:
- Satellite connections:satellite连接用来传递session中的相邻item间的信息。论文中使用GGNN为例,实现相邻节点之间的信息传播,并且按照satellite边构建输入和输出矩阵,例如对于session ,构建的输入输出矩阵如图3:
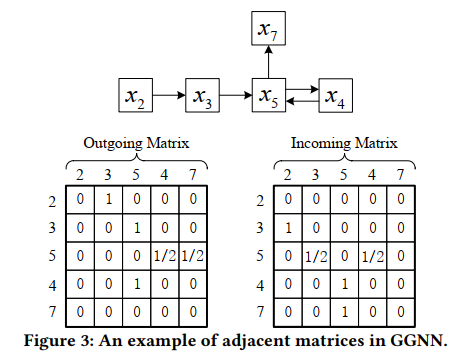
- Star connections:受Star-Transformer模型启发,在图中添加Star节点,构建星型图。star节点和satellite节点之间的边就是Star连接,如图2,Star连接是双向边,分别代表两种信息传递方向,更新两种节点。一方面,以star节点作为中间节点,非相邻的item之间能够以two-hop的方式进行信息传播,来更新satellite节点。另一方面,另一个方向的边能够用来考虑所有satellite节点的信息,生成准确的star节点表示。
本文模型使用门控网络控制分别从邻居节点和star节点获取信息量的多少。
3.3 学习item嵌入
学习satellite节点和star节点表示
3.3.1 初始化
- satellite节点:使用item的embedding
- star节点:对satellite节点进行平均池化,得到star节点初始状态
3.3.2 更新节点
1、Satellite节点更新
对于每个satellite节点,邻居节点信息包括相邻节点信息和star节点信息,分别对应来自直接相连节点和没有直接相连节点的信息。
首先,考虑相邻节点信息,使用GGNN网络更新节点。对于图的第层每个satellite节点,使用出度和入度矩阵获得传播的信息:
其中,,分别为入度和出度矩阵的第行,是参数矩阵,是偏置向量。最终得到的表示节点的传播信息,然后继续使用GGNN网络计算:
其中,,是参数矩阵,表示sigmoid激活函数,表示向量的对应元素点乘。使用这种方式,相邻节点的信息能够在星型图中传播。
然后,考虑来自star节点的信息,对于每个satellite节点,使用门控机制考虑应该从相邻节点和star节点分别获取多少信息。具体来说,使用自注意力计算和star节点的相似度:
其中,是参数矩阵,是的表示向量。然后计算最终的节点表示:
注意,这里的star节点是上一层的,因为这一层的star节点还没有更新,star节点需要在satellite节点更新完之后再更新。
2、Star节点更新
star节点是根据最新的satellite节点表示来更新的,同样使用self-attention,将star节点作为Query向量:
是对应的参数矩阵。最后计算得到star节点的向量表示
其中,
3.3.3 Highway Networks
上述节点更新的过程可以多次迭代,即堆叠多层SGNN,第层SGNN可以表示为:
多层图结构可以传播大量节点间的信息,同样也会带来偏差,导致过拟合,为了处理这个问题,使用highway networks从多层SGNN之前和之后选择性地获取信息。
用分别表示多层SGNN之前和多层SGNN之后的satellite节点表示,HN网络用以下公式表示:
其中,是由SGNN的输入输出决定的:
。
HN网络处理之后,得到satellite节点和star节点的最终表示和(简写为)。将以上步骤用算法流程表示:


评估指标使用Precision和MRR。
五、实验结果
5.1 与SOTA模型对比
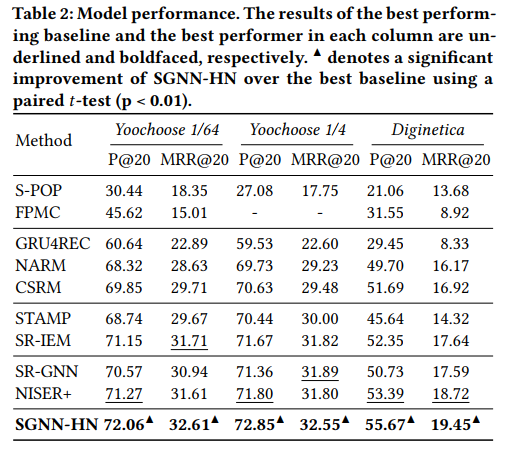
5.2 SGNN网络的作用
分别用自注意力网络(SAT)和门控图神经网络(GGNN)代替SGNN:
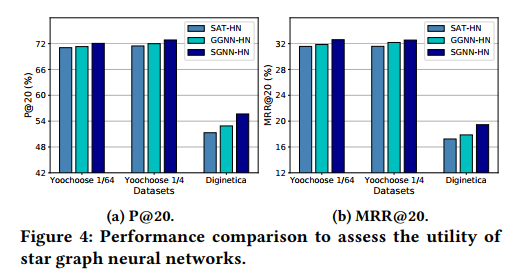
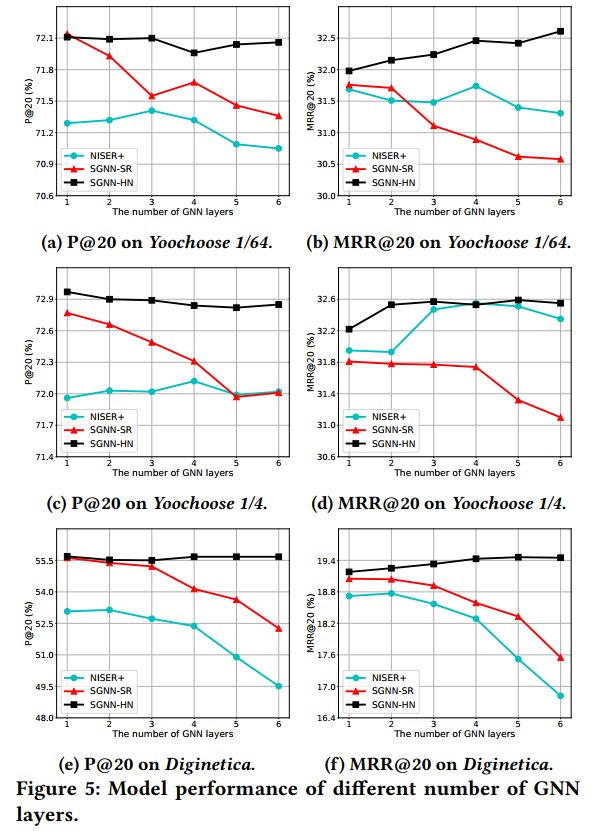
5.3 HN网络层的作用
HN网络对于不同数量GNN层的作用:
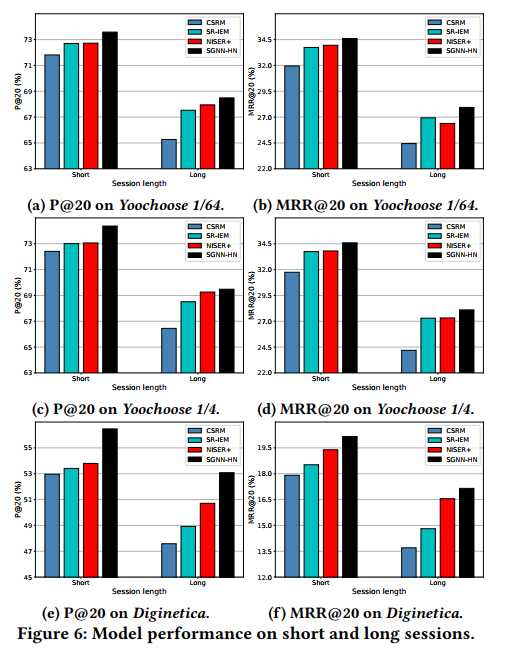
5.4 Session长度的影响
六、结论
本文提出了SGNN-HN模型,一方面解决了一般GNN模型不能考虑高阶信息转换的问题,另一方面解决了GNN模型容易过拟合的问题。
- 本文作者:Kangshitao
- 本文链接:http://kangshitao.github.io/2020/11/05/paper-SGNN-HN/index.html
- 版权声明:本博客所有文章均采用 BY-NC-SA 许可协议,转载请注明出处!
